Alt-Ergo @ OCamlPro: Two months later

---

As announced in a previous post, I joined OCamlPro at the beginning of September and I started working on Alt-Ergo. Here is a report presenting the tool and the work we have done during the two last months.

Alt-Ergo at a Glance

Alt-Ergo is an open source automatic theorem prover based on SMT technology. It is developed at Laboratoire de Recherche en Informatique, Inria Saclay Ile-de-France and CNRS since 2006. It is capable of reasoning in a combination of several built-in theories such as uninterpreted equality, integer and rational arithmetic, arrays, records, enumerated data types and AC symbols. It also handles quantified formulas and has a polymorphic first-order native input language. Alt-Ergo is written in OCaml. Its core has been formally proved in the Coq proof assistant.

Alt-Ergo has been involved in a qualification process (DO-178C) by Airbus Industrie. During this process, a qualification kit has been produced. It was composed of a technical document with tool requirements (TR) that gives a precise description of each part of the prover, a companion document (~ 450 pages) of tests, and an instrumented version of the tool with a TR trace mechanism.

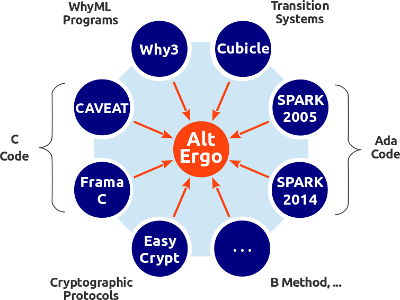
Alt-Ergo Spider Web

Alt-Ergo is mainly used to prove the validity of mathematical formulas generated by program verification platforms. It was originally designed and tuned to prove formulas generated by the Why tool. Now, it is used by different tools and in various contexts, in particular via the Why3 platform. As shown by the diagram below, Alt-Ergo is used to prove formulas:

• generated from Ada code by SPARK 2005 and SPARK 2014,
• generated from C programs by Frama-C and CAVEAT,
• produced from WhyML programs by Why3,
• translated from proof obligations generated by Atelier-B,

Moreover, Alt-Ergo is used in the context of cryptographic protocols verification by EasyCrypt and in SMT-based model checking by Cubicle.

Some "Hello World" Examples

Below are some basic formulas written in the why input syntax. Each example is proved valid by Alt-Ergo. The first formulas is very simple and is proved with a straightforward arithmetic reasoning. goal g2 requires reasoning in the combination of functional arrays and linear arithmetic, etc. The last example contains a quantified sub-formula with a polymorphic variable x. Generating four ground instances of this axiom where x is replaced by 1, true, 1.4 and a respectively is necessary to prove goal g5.

** Simple arithmetic operation **

goal g1 : 1 + 2 = 3

** Theories of functional arrays and linear integer arithmetic **

logic a : (int, int) farray
goal g2 : forall i:int. i = 6 -> a[i<-4][5] = a[i-1]

** Theories of records and linear integer arithmetic **

type my_record = { a : int ; b : int }
goal g3 : forall v,w : my_record. 2 * v.a = 10 -> { v with b = 5} = w -> w.a = 5

** Theories of enumerated data types and uninterpreted equality **

type my_sum = A | B | C
logic P : 'a -> prop
goal g4 : forall x : my_sum. P(C) -> x<>A and x<>B -> P(x)

** Formula with quantifiers and polymorphism **

axiom a: forall x : 'a. P(x)
goal g5 : P(1) and P(true) and P(1.4) and P(a)

** formula with quantifiers and polymorphism **

$$ alt-ergo examples.why
File "examples.why", line 2, characters 1-21:Valid (0.0120) (0)
File "examples.why", line 6, characters 1-53:Valid (0.0000) (1)
File "examples.why", line 10, characters 1-81:Valid (0.0000) (3)
File "examples.why", line 15, characters 1-59:Valid (0.0000) (6)
File "examples.why", line 19, characters 1-47:Valid (0.0000) (10)

Alt-Ergo @ OCamlPro

On September 20, we officially announced the distribution and the support of Alt-Ergo by OCamlPro and launched its new website. This site allows to download public releases of the prover and to discover available support offerings. It'll be enriched with additional content progressively. The former Alt-Ergo's web page hosted by LRI is now devoted to theoretical foundations and academic aspects of the solver.

We have also published a new public release (version 0.95.2) of Alt-Ergo. The main changes in this minor release are: source code reorganization into sub-directories, simplification of quantifiers instantiation heuristics, GUI improvement to reduce latency when opening large files, as well as various bug fixes.

In addition to the re-implementation and the simplification of some parts of the prover (e.g. internal literals representation, theories combination architecture, ...), the main novelties of the current master branch of Alt-Ergo are the following:

• The user can now specify an external (plug-in) SAT-solver instead of the default DFS-based engine. We experimentally provide a CDCL solver based on miniSAT that can be plugged to perform satisfiability reasoning. This solver is more efficient when formulas contain a rich propositional structure.
• We started the development of a new tool, called Ctrl-Alt-Ergo, in which we put our expertise by implementing the most interesting strategies of Alt-Ergo. The experiments we made with our internal benchmarks are very promising, as shown below.

Experimental Evaluation

We compared the performances of latest public releases of Alt-Ergo with the current master branch of both Alt-Ergo and Ctrl-Alt-Ergo (commit ce0bba61a1fd234b85715ea2c96078121c913602) on our internal test suite composed of 16209 formulas. Timeout was set to 60 seconds and memory was limited to 2GB per formula. Benchmarks descriptions and the results of our evaluation are given below.

Why3 Benchmark

This benchmark contains 2470 formulas generated from Why3's gallery of WhyML programs. Some of these formulas are out of scope of current SMT solvers. For instance, the proof of some of them requires inductive reasoning.

SPARK Hi-lite Benchmark

This benchmark is composed of 3167 formulas generated from Ada programs used during Hi-lite project. It is known that some formulas are not valid.

BWare Benchmark

This test-suite contains 10572 formulas translated from proof obligations generated by Atelier-B. These proof obligations are issued from industrial B projects and are proved valid.

	Alt-Ergo version 0.95.1	Alt-Ergo version 0.95.2	Alt-Ergo master branch*	Ctrl-Alt-Ergo master branch*
Release date	Mar. 05, 2013	Sep. 20, 2013	– – –	– – –
Why3 benchmark	2270 (91.90 %)	2288 (92.63 %)	2308 (93.44 %)	2363 (95.67 %)
SPARK benchmark	2351 (74.23 %)	2360 (74.52 %)	2373 (74.93 %)	2404 (75.91 %)
BWare benchmark	5609 (53.05 %)	9437 (89.26 %)	10072 (95.27 %)	10373 (98.12 %)

(*) commit `ce0bba61a1fd234b85715ea2c96078121c913602`

---

About Alt-Ergo

Alt-Ergo is an Open Source automatic solver of mathematical formulas designed for program verification. Alt-Ergo is very successful for proving formulas generated in the context of deductive program verification. It was originally designed and tuned to be used by the Why3 platform. Its development started in 2006 at the Laboratoire de Recherche en Informatique (LRI - CNRS/Inria) of the Université Paris-Saclay and is maintained, developed and distributed since 2013 by the Formal Methods team at OCamlPro.

This work is made possible through research projects like Décysif, Soprano, BWare, Vocal and LCHIP, as well as support from our Alt-Ergo Users' Club members. If Alt-Ergo has been valuable to you, consider joining the Alt-Ergo Users' Club.