OCamlPro’s Liquidity-lang demo at JFLA2018 – a smart-contract design language
As a tradition, we took part in this year's Journées Francophones des Langages Applicatifs (JFLA 2018) that was chaired by LRI's Sylvie Boldo and hosted in Banyuls the last week of January. That was a nice opportunity to present a live demo of a multisignature smart-contract entirely written in the Liquidity language designed at OCamlPro, and deployed live on the Tezos alphanet (the slides are now available, see at the end of the post).
Tezos is the only blockchain to use a strongly typed, functional language, with a formal semantic and an interpreter validated by the use of GADTs (generalized abstract data-types). This stack-based language, named Michelson, is somewhat tricky to use as-is, the absence of variables (among others) necessitating to manipulate the stack directly. For this reason, we have developed, starting in June 2017, a higher level language, Liquidity, implementing the type system of Michelson in a subset of OCaml.
In addition to the compiler which allows to compile Liquidity programs to Michelson ones, we have developed a decompiler which, from Michelson code, can recover a Liquidity version, much easier to look at and understand (for humans). This tool is of some significance considering that contracts will be stored on the blockchain in Michelson format, making them more approachable and understandable for end users.
To facilitate designing contracts and foster Liquidity adoption we have also developed a web application. This app offers somewhat bare-bone editors for Liquidity and Michelson, allows compilation in the browser directly, deployment of Liquidity contracts and interaction with them (using the Tezos alphanet).
This blog post presents these different tools in more detail.
Michelson
Michelson is a stack-based, functional, statically and strongly typed language. It comes with a set of built-in base types like strings, Booleans, unbounded integers and naturals, lists, pairs, option types, union (of two) types, sets, maps. There also a number of domain dependent types like amounts (in tezzies), cryptographic keys and signatures, dates, etc. A Michelson program consists in a structured sequence of instructions, each of which operates on the stack. The program takes as inputs a parameter as well as a storage and returns a result and a new value for the storage. They can fail at runtime with the instruction FAIL, or another error (call of a failing contract, out of gas, etc.), but most instructions that could fail return an option instead ( e.g EDIV returns None when dividing by zero). The following example is a smart contract which implements a voting system on the blockchain. The storage consists in a map from possible votes (as strings) to integers counting number of votes. A transaction to this contract must be made with an amount (accessible with instruction AMOUNT) greater or equal to 5 tezzies and a parameter which is a valid vote. If one of these conditions is not respected, the execution, and thus the transaction, fail. Otherwise the program retrieves the previous number of votes in the storage and increments them. At the end of the execution, the stack contains the pair composed of the value Unit and the updated map (the new storage).
parameter string;
storage (map string int);
return unit;
code
{ # Pile = [ Pair parameter storage ]
PUSH tez "5.00"; AMOUNT; COMPARE; LT;
IF # Is AMOUNT < 5 tz ?
{ FAIL }
{
DUP; DUP; CAR; DIP { CDR }; GET; # GET parameter storage
IF_NONE # Is it a valid vote ?
{ FAIL }
{ # Some x, x now in the stack
PUSH int 1; ADD; SOME; # Some (x + 1)
DIP { DUP; CAR; DIP { CDR } }; SWAP; UPDATE;
# UPDATE parameter (Some (x + 1)) storage
PUSH unit Unit; PAIR; # Pair Unit new_storage
}
};
}
Michelson has several specificities:
- Typing a Michelson program is done by types propagation, and not à la Milner. Polymorphic types are forbidden and type annotations are required when a type is ambiguous ( e.g. empty list).
- Functions (lambdas) are pure and are not closures, i.e. they must have an empty environment. For instance, a function passed to another contract as parameter acts in a purely functional way, only accessing the environment of the new contract.
- Method calls is preformed with the instruction
TRANSFER_TOKENS: it requires an empty stack (not counting its arguments). It takes as argument the current storage, saves it before the call is made, and finally returns it after the call together with the result. This forces developers to save anything worth saving in the current storage, while keeping in mind that a reentring call can happend (the returned storage might be different).
We won't explain the semantics of Michelson here, a good one in big step form is available here.
The Liquidity Language
Liquidity is also a functional, statically and strongly typed language that compiles down to the stack-based language Michelson. Its syntax is a subset of OCaml and its semantic is given by its compilation schema (see below). By making the choice of staying close to Michelson in spirit while offering higher level constraints, Liquidity allows to easily write legible smart contracts with the same safety guaranties offered by Michelson. In particular we decided that it was important to keep the purely functional aspect of the language so that simply reading a contract is not obscured by effects and global state. In addition, the OCaml syntax makes Liquidity an immediately accessible tool to programmers who already know OCaml while its limited span makes the learning curve not too steep.
The following example is a liquidity version of the vote contract. Its inner workings are rather obvious for anyone who has already programmed in a ML-like language.
[%%version 0.15]
type votes = (string, int) map
let%init storage (myname : string) =
Map.add myname 0 (Map ["ocaml", 0; "pro", 0])
let%entry main
(parameter : string)
(storage : votes)
: unit * votes =
let amount = Current.amount() in
if amount < 5.00tz then
Current.failwith "Not enough money, at least 5tz to vote"
else
match Map.find parameter storage with
| None -> Current.failwith "Bad vote"
| Some x ->
let storage = Map.add parameter (x+1) storage in
( (), storage )
A Liquidity contract starts with an optional version meta-information. The compiler can reject the program if it is written in a too old version of the language or if it is itself not recent enough. Then comes a set of type and function definitions. It is also possible to specify an initial storage (constant, or a non-constant storage initializer) with let%init storage. Here we define a type abbreviation votes for a map from strings to integers. It is the structure that we will use to store our vote counts.
The storage initializer creates a map containing two bindings, "ocaml" to 0 and "pro" to 0 to which we add another vote option depending on the argument myname given at deploy time.
The entry point of the program is a function main defined with a special annotation let%entry. It takes as arguments a call parameter (parameter) and a storage (storage) and returns a pair whose first element is the result of the call, and second element is a potentially modified storage.
The above program defines a local variable amount which contains the amount of the transaction which generated the call. It checks that it is greater than 5 tezzies. If not, we fail with an explanatory message. Then the program retrieves the number of votes for the chosen option given as parameter. If the vote is not a valid one (i.e., there is no binding in the map), execution fails. Otherwise, the current number of votes is bound to the name x. Storage is updated by incrementing the number of votes for the chosen option. The built-in function Map.add adds a new binding (here, it replaces a previously existing binding) and returns the modified map. The program terminates, in the normal case, on its last expression which is its returned value (a pair containing () the contract only modifies the storage and the storage itself).
A reference manual for Liquidity is available here. It gives a relatively complete overview of the available types, built-in functions and constructs of the language.
Compilation
Encodings
Because Liquidity is a lot richer than Michelson, some types and constructs must be simplified or encoded. Record types are translated to right-associated pairs with as many components as the record has fields. t1 is encoded as t1' in the following example.
type t1 = { a: int; b: string; c: bool}
type t1’ = (int * (string * bool))
Field accesses in a record is translated to accesses in the corresponding tuples (pairs). Sum (or union) types are translated using the built-in variant type (this is the or type in Michelson). t2 is encoded as t2' in the following example.
type ('a, 'b) variant = Left of 'a | Right of `b
type t2 = A of int | B of string | C
type t2’ = (int, (string, unit) variant) variant
Similarly, pattern matching on expressions of a sum type is translated to nested pattern matchings on variant typed expressions. An example translation is the following:
match x with
| A i -> something1(i)
| B s -> something2(s)
| C -> something3
match x with
| Left i -> something1(i)
| Right r -> match r with
| Left s -> something2(s)
| Right -> something3
Liquidity also supports closures while Michelson only allows pure lambdas. Closures are translated by lambda-lifting, i.e. encoded as pairs whose first element is a lambda and second element is the closure environment. The resulting lambda takes as argument a pair composed of the closure's argument and environment. Adequate transformations are also performed for built-in functions that take lambdas as arguments ( e.g. in List.map) to allow closures instead.
Compilation schema
This little section is a bit more technical, so if you don't care how Liquidity is compiled precisely, you can skip over to the next one.
We note by Γ, [|x|]d ⊢ X ↑t compilation of the Liquidity instruction x, in environment Γ. Γ is a map associating variable names to a position in the stack. The compilation algorithm also maintains the size of the current stack (at compilation of instruction x), denoted by d in the previous expression. Below is a non-deterministic version of the compilation schema, the one implemented in the Liquidity compiler being a determinized version.

The result of compiling x is a Michelson instruction (or sequence of instructions) X together with a Boolean transfer information t. The instruction Contract.call (or TRANSFER_TOKENS in Michelson) needs an empty stack to evaluate, so the compiler empties the stack before translating this call. However, the various branches of a Michelson program must have the same stack type. This is why we need to maintain this information so that the compiler can empty stacks in some parts of the program.
Some of the rules have parts annotated with ?b. This suffix denotes a potential reset or erasing. In particular:
- For sets, Γ?*b is ∅ if b evaluates to false, and Γ otherwise.
- For integers, *d?b is
0if b evaluates to false, and d otherwise. - For instructions, (*X)?b is
{}if b evaluates to false, and X otherwise.
For instance, by looking at rule CONST, we can see that compiling a Liquidity constant simply consists in pushing this constant on the stack. To handle variables in a simple manner, the rule VAR tells us to look in the environment Γ for the index associated to the variable we want to compile. Then, instruction D(U)iP puts at the top of the stack a copy of the element present at depth i. Variables are added to Γ with the Liquidity instruction let ... in or with any instruction that binds an new symbol, like fun for instance.
Decompilation from Michelson
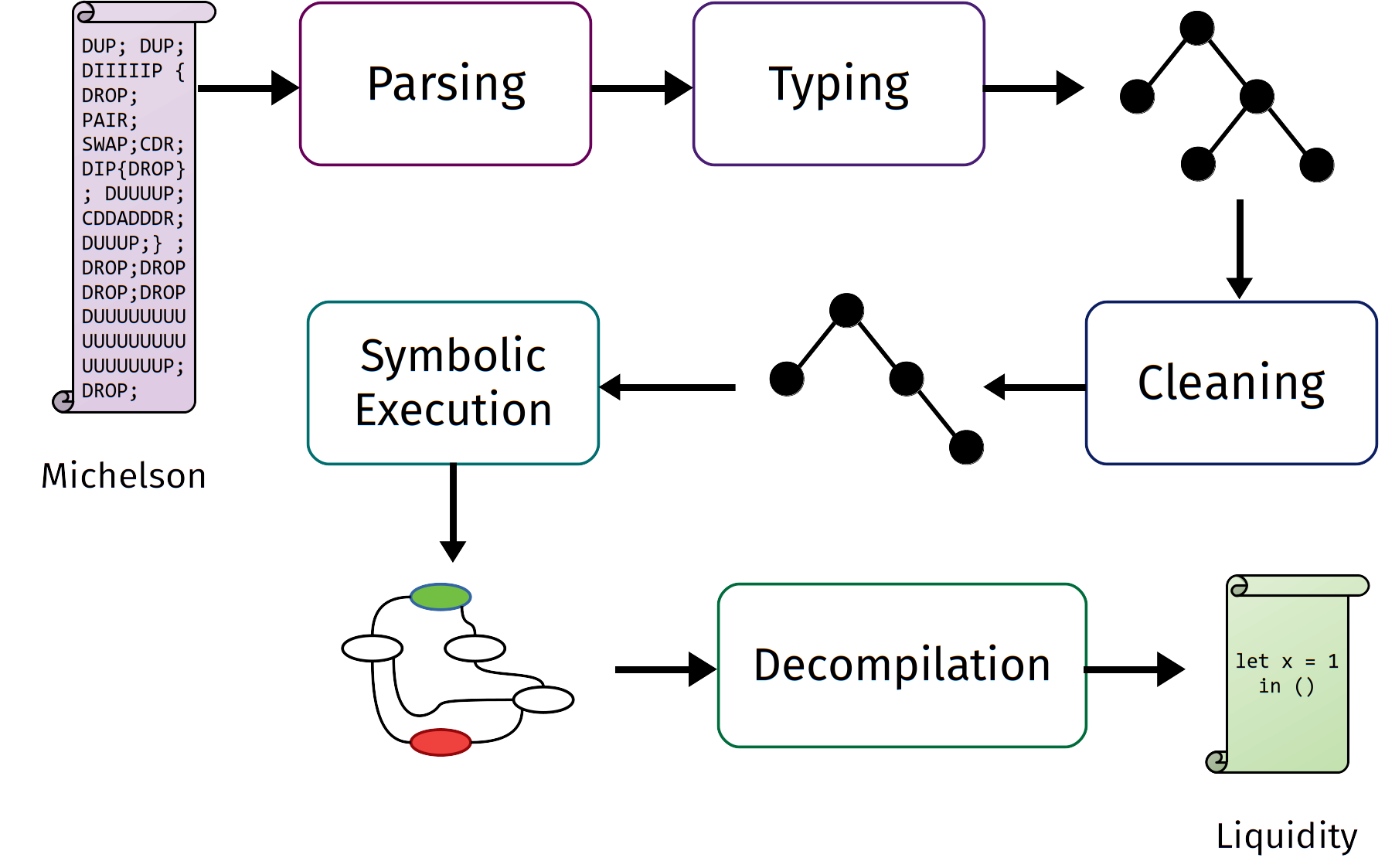
While Michelson programs are high level compared to other bytecodes, it remains difficult for a blockchain end-user to understand what a Michelson program does exactly by looking at it. However, following the idea that "code is law", a user should be able to read a contract and understand its precise semantic. Thus, we have developed a decompiler from Michelson to Liquidity, which allows to recover a much more readable and understandable representation of a program on the blockchain.
The decompilation of Michelson code follows the diagram below where:
- Cleaning consists in simplifying Michelson code to accelerate the whole process and simplify the following task. For now it consists in ereasing instructions whose continuation is a failure.
- Symbolic Execution consists in executing the Michelson program with symbolic inputs, and by replacing every value placed in the stacj by a node containing the instruction that generated it. Each node of this graph can be seen as an expression of the target program, which can be bound to a variable name. Edges to this node represent future occurrences of this variable.
- Decompilation consists in transforming the graph generated by the previous step in a Liquidity syntax tree. Names for variables are recovered from annotations produced by the Liquidity compiler (in case we decompile a Michelson program that was generated from Liquidty), or are chosen on the fly when no annotation is present (e.g. if the Michelson program was written by hand).
Finally the program is typed (to ensure no mistakes were made), simplified and pretty printed.
Example of decompilation
return int;
storage int;
code {DUP; CAR;
DIP { CDR; PUSH int 1 }; # stack is: parameter :: 1 :: storage
IF # if parameter = true
{ DROP; DUP; } # stack is storage :: storage
{ } # stack is 1 :: storage
;
PAIR;
}
This example illustrate some of the difficulties of the decompilation process: Liquidity is a purely functional language where each construction is an expression returning a value; Michelson handles the stack directly, which is impossible to concretize in in Liquidity (values in the stack don't have the same type, as opposed to values in a list). In this example, depending on the value of parameter the contract returns either the content of the storage, or the integer 1. In the Michelson code, the programmer used the instruction IF, but its branches do not return a value and only operates by modifying (or not) the stack.
[%%version 0.15]
type storage = int
let%entry main (parameter : bool) (storage : storage) : (int * storage) =
((if parameter then storage else 1 ), storage)
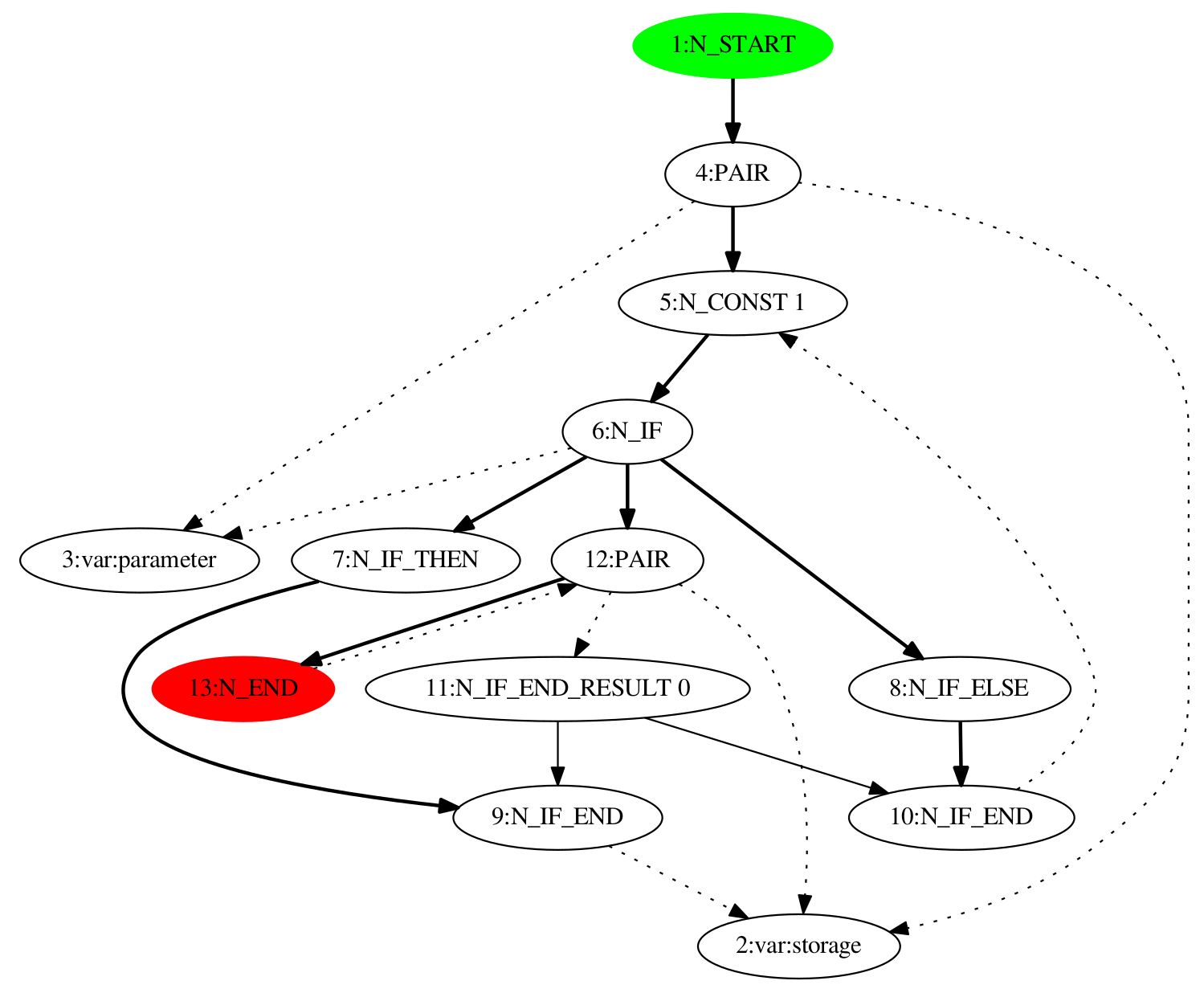
The above translation to Liquidity also contains an if, but it has to return a value. The graph below is the result of the symbolic execution phase on the Michelson program. The IF instruction is decomposed in several nodes, but does not contain any remaining instruction: the result of this if is in fact the difference between the stack resulting from the execution of the then branch and from the else branch. It is denoted by the node N_IF_END_RESULT 0 (if there were multiple of these nodes with different indexes, the result of the if would have been a tuple, corresponding to the multiple changes in the stack).
Try-Liquidity
You can go to https://liquidity-lang.org/edit to try out Liquidity in your browser.
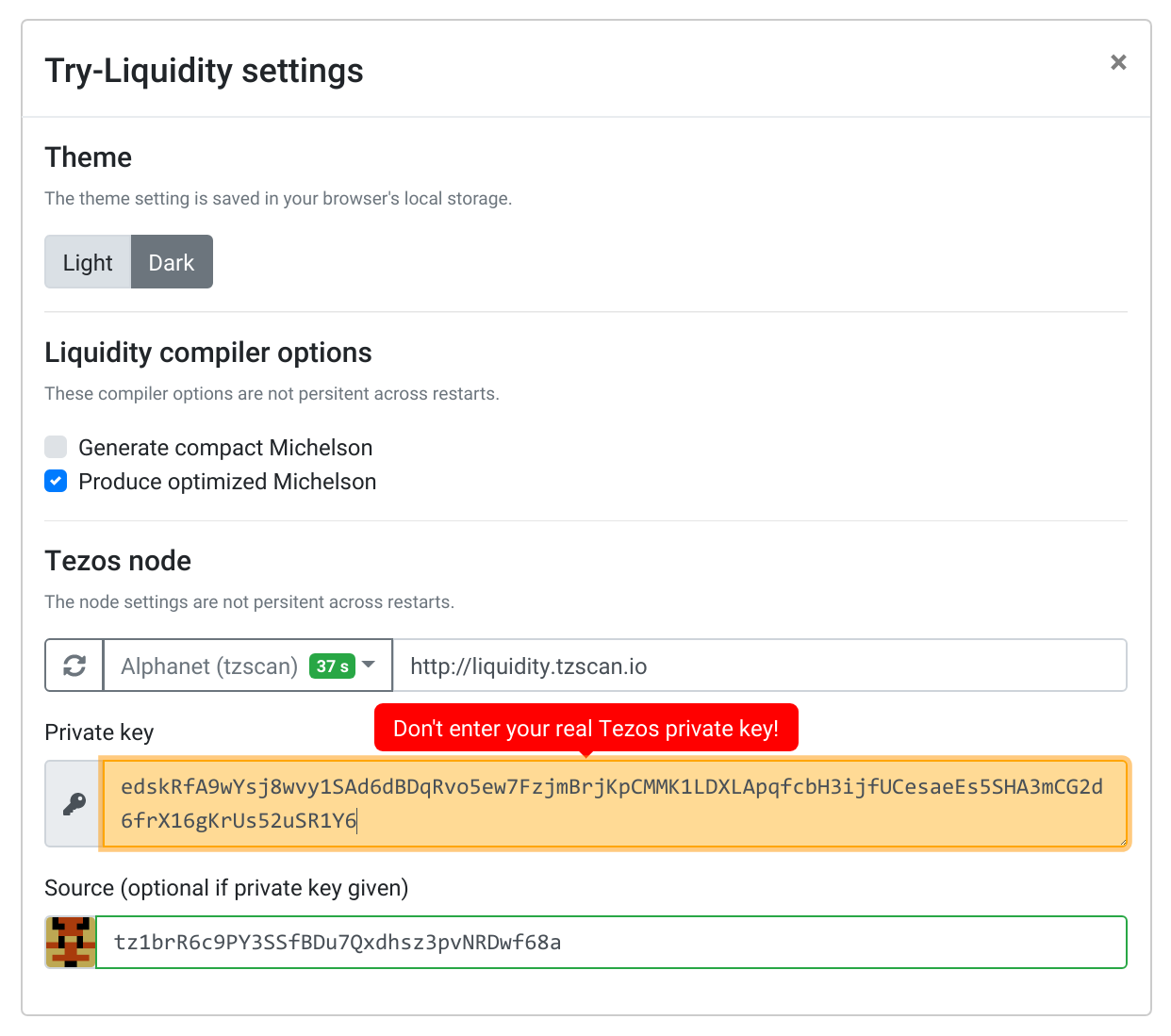
The first thing to do (if you want to deploy and interact with a contract) is to go into the settings menu. There you can set your Tezos private key (use one that you generated for the alphanet for the moment) or the source (i.e. your public key hash, which is derived from your private key if you set it).
You can also change which Tezos node you want to interact with (the first one should do, but you can also set one of your choosing such as one running locally on your machine). The timestamp shown next to the node name indicates how long ago was produced the last block that it knows of. Transactions that you make on a node that is not synchronized will not be included in the main chain.
 You should now see your account with its balance in the top bar:
You should now see your account with its balance in the top bar:

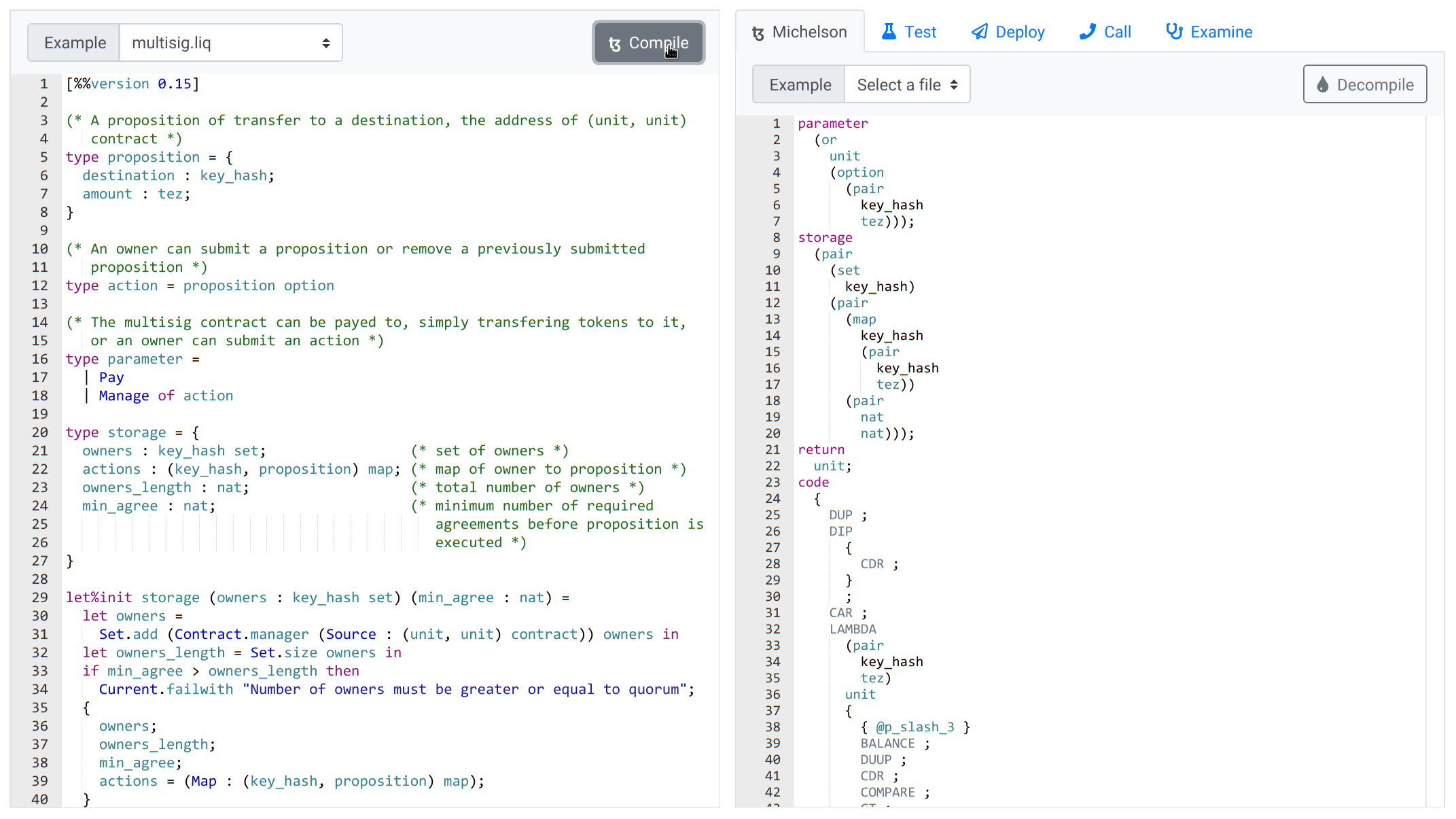
In the main editor window, you can select a few Liquidity example contracts or write your own. For this small tutorial, we will select multisig.liq which is a minimal multi-signature wallet contract. It allows anyone to send money to it, but it requires a certain number of predefined owners to agree before making a withdrawal.
Clicking on the button Compile should make the editor blink green (when there are no errors) and the compiled Michelson will appear on the editor on the right.
 Let's now deploy this contract on the Tezos alphanet. By going into the Deploy (or paper airplane icon) tab, we can choose our set of owners for the multisig contract and the minimum number of owners to be in agreement before a withdrawal can proceed. Here I put down two account addresses for which I possess the private keys, and I want the two owners to agree before any transaction is approved (
Let's now deploy this contract on the Tezos alphanet. By going into the Deploy (or paper airplane icon) tab, we can choose our set of owners for the multisig contract and the minimum number of owners to be in agreement before a withdrawal can proceed. Here I put down two account addresses for which I possess the private keys, and I want the two owners to agree before any transaction is approved (2p is the natural number 2).
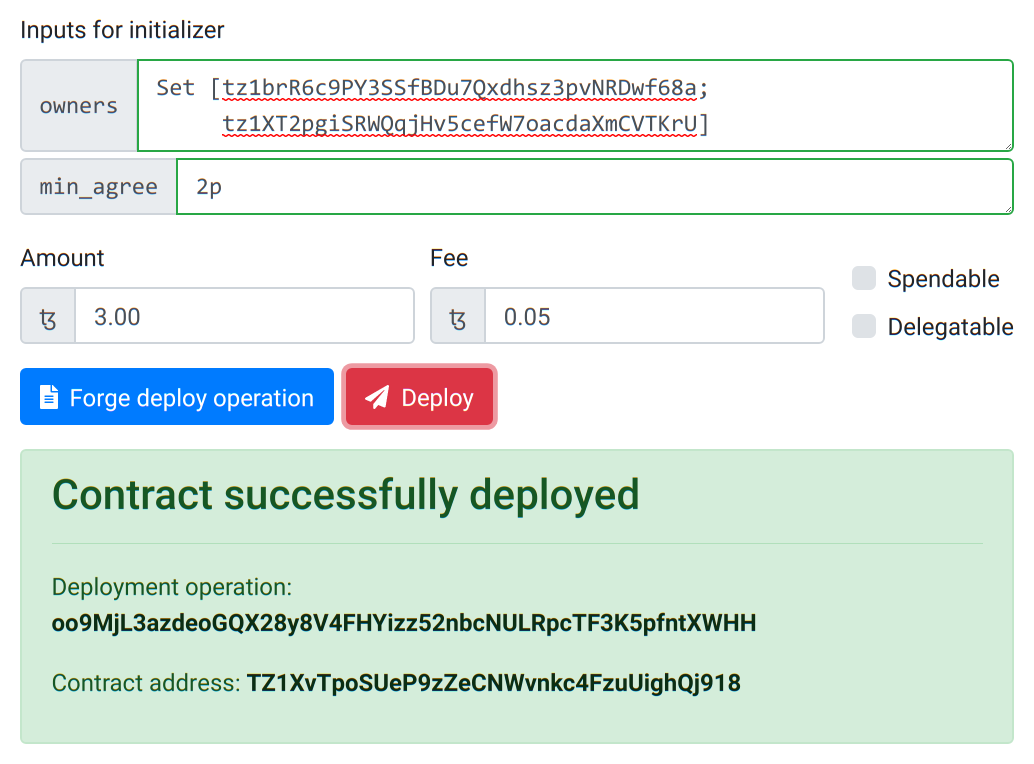 Then I can either forge the deployment operation which is then possible to sign offline and inject in the Tezos chain by other means, or I can directly deploy this contract (if the private key is set in settings). If deployment is successful, we can see both the deployment operation and the new contract on a block explorer by clicking on the provided links.
Then I can either forge the deployment operation which is then possible to sign offline and inject in the Tezos chain by other means, or I can directly deploy this contract (if the private key is set in settings). If deployment is successful, we can see both the deployment operation and the new contract on a block explorer by clicking on the provided links.
Now we can query the blockchain to examine our newly deployed contract. Head over to the Examine tab. The address field should already be filled with our contract handle. We just have to click on Retrieve balance and storage.
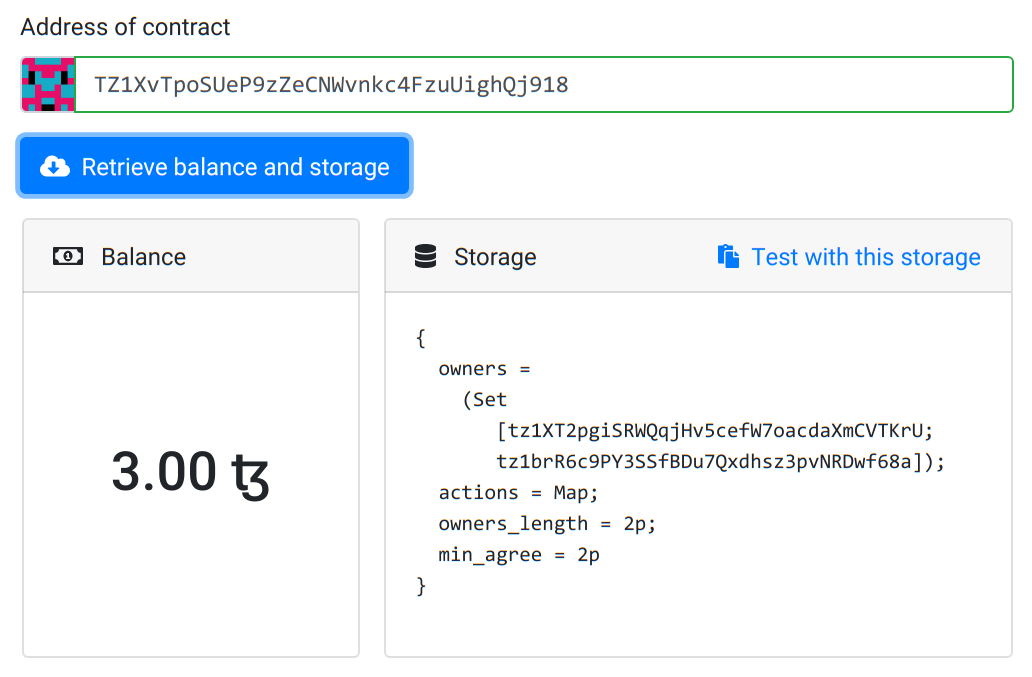 The contract has 3tz on its balance because we chose to initialize it this way. On the right is the current storage of the contract (in Liquidity syntax) which is a record with four fields. Notice that the
The contract has 3tz on its balance because we chose to initialize it this way. On the right is the current storage of the contract (in Liquidity syntax) which is a record with four fields. Notice that the actions field is an empty map.
Let's make a few calls to this contract. Head over to the Call tab and fill-in the parameter and the amount. We can send for instance 5.00tz with the parameter Pay. Clicking on the button Call generates a transaction which we can observe on a block explorer. More importantly if we go back to the Examine tab, we can now retrieve the new information and see that the storage is unchanged but the balance is 8.00tz.
We can also make a call to withdraw money from the contract. This is done by passing a parameter of the form:
Manage (
Some {
destination = tz1brR6c9PY3SSfBDu7Qxdhsz3pvNRDwf68a;
amount = 2tz;
})
This is a proposition of transfer of funds in the amount of 2.00tz from the contract to the destination tz1brR6c9PY3SSfBDu7Qxdhsz3pvNRDwf68a.
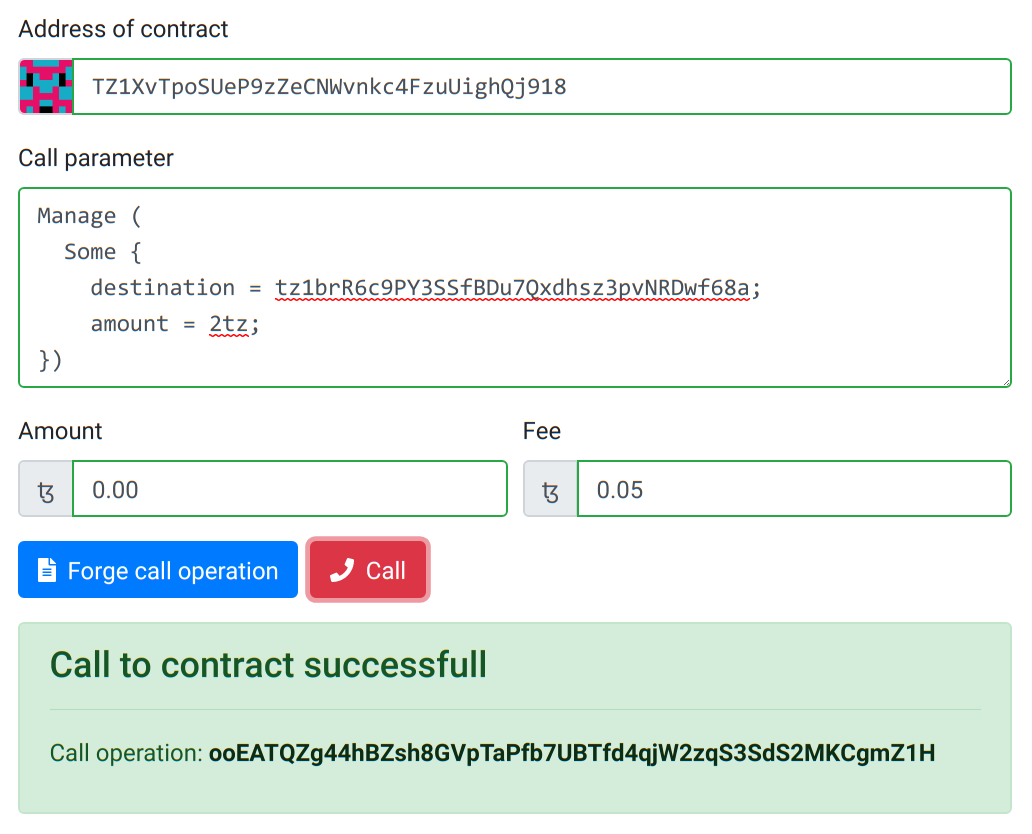
The balance of the contract has not changed (it is still 8.00tz) but the storage has been modified. That is because this multisig contract requires two owners to agree before proceeding. The proposition is stored in the map actions and is associated to the owner who made said proposition.
{
owners =
(Set
[tz1XT2pgiSRWQqjHv5cefW7oacdaXmCVTKrU;
tz1brR6c9PY3SSfBDu7Qxdhsz3pvNRDwf68a]);
actions =
(Map
[(tz1brR6c9PY3SSfBDu7Qxdhsz3pvNRDwf68a,
{
destination = tz1brR6c9PY3SSfBDu7Qxdhsz3pvNRDwf68a;
amount = 2.00tz
})]);
owners_length = 2p;
min_agree = 2p
}
We can now open a new browser tab and point it to https://liquidity-lang.org/edit, but this time we fill in the private key for the second owner tz1XT2pgiSRWQqjHv5cefW7oacdaXmCVTKrU. We choose the multisig contract in the Liquidity editor and fill-in the contract address in the call tab with the same one as in the other session TZ1XvTpoSUeP9zZeCNWvnkc4FzuUighQj918 (you can double check the icons for the two contracts are identical). For the the withdrawal to proceed, this owner has to make the exact same proposition so let's make a call with the same parameter:
Manage (
Some {
destination = tz1brR6c9PY3SSfBDu7Qxdhsz3pvNRDwf68a;
amount = 2tz;
})
The call should also succeed. When we examine the contract, we can now see that its balance is down to 6.00tz and that the field actions of its storage has been reinitialized to the empty map. In addition, we can update the balance of our first account (by clicking on the circle arrow icon in the tob bar) to see that it is now up an extra 2.00tz and that was the destination of the proposed (and agreed on) withdrawal. All is well!
We have seen how to compile, deploy, call and examine Liquidity contracts on the Tezos alphanet using our online editor. Experiment with your own contracts and let us know how that works for you!
Comments
fredcy (9 February 2018 at 3 h 14 min):
It says “Here we define a type abbreviation votes […]” but I don’t see any
votessymbol in the nearby code.[Still working through the document. I’m eager to try Liquidity rather than write in Michelson.]
alain (9 February 2018 at 7 h 18 min):
You are right, thanks for catching this. I’ve updated the contract code to use type
votes.
branch (26 February 2019 at 18 h 28 min):
Why the “Deploy” button can be inactive, while liquidity contract is compiled successfully?
alain (6 March 2019 at 15 h 09 min):
For the Deploy button to become active, you need to specify an initial value for the storage directly in the code of the smart contract. This can be done by writing a constant directly or a function.
let%init storage = (* the value of your initial storage*)
let%init storage x y z = (* the value of your initial storage, function of x, y and z *)
Au sujet d'OCamlPro :
OCamlPro développe des applications à haute valeur ajoutée depuis plus de 10 ans, en utilisant les langages les plus avancés, tels que OCaml, Rust, et WebAssembly (Wasm) visant aussi bien rapidité de développement que robustesse, et en ciblant les domaines les plus exigeants (méthodes formelles, cybersécurité, systèmes distribués/blockchain, conception de DSLs). Fort de plus de 20 ingénieurs R&D, avec une expertise unique sur les langages de programmation, aussi bien théorique (plus de 80% de nos ingénieurs ont une thèse en informatique) que pratique (participation active au développement de plusieurs compilateurs open-source, prototypage de la blockchain Tezos, etc.), diversifiée (OCaml, Rust, Cobol, Python, Scilab, C/C++, etc.) et appliquée à de multiples domaines. Nous dispensons également des [formations sur mesure certifiées Qualiopi sur OCaml, Rust, et les méthodes formelles] (https://training.ocamlpro.com/) Pour nous contacter : contact@ocamlpro.com.
Articles les plus récents
2025
2024
- opam 2.3.0 release!
- Optimisation de Geneweb, 1er logiciel français de Généalogie depuis près de 30 ans
- Alt-Ergo 2.6 is Out!
- Flambda2 Ep. 3: Speculative Inlining
- opam 2.2.0 release!
- Flambda2 Ep. 2: Loopifying Tail-Recursive Functions
- Fixing and Optimizing the GnuCOBOL Preprocessor
- OCaml Backtraces on Uncaught Exceptions
- Opam 102: Pinning Packages
- Flambda2 Ep. 1: Foundational Design Decisions
- Behind the Scenes of the OCaml Optimising Compiler Flambda2: Introduction and Roadmap
- Lean 4: When Sound Programs become a Choice
- Opam 101: The First Steps
2023