CPS Representation and Foundational Design Decisions in Flambda2
In this first post of the Flambda2 Snippets, we dive into the powerful CPS-based internal representation used within the Flambda2 optimizer, which was one of the main motivation to move on from the former Flambda optimizer.
Credit goes to Andrew Kennedy's paper Compiling with Continuations, Continued for pointing us in this direction.
CPS (Continuation Passing Style)
Terms in the Flambda2 IR are represented in CPS style, so let us briefly
explain what that means.
Some readers may already be familiar with what we call First-Class CPS where continuations are represented using functions of the language:
(* Non-tail-recursive implementation of map *)
let rec map f = function
| [] -> []
| x :: r -> f x :: map f r
(* Tail-recursive CPS implementation of map *)
let rec map_cps f l k =
match l with
| [] -> k []
| x :: r -> let fx = f x in map_cps f r (fun r -> fx :: r)
This kind of transformation is useful to make a recursive function tail-recursive and sometimes to avoid allocations for functions returning multiple values.
In Flambda2, we use Second-Class CPS instead, where continuations are
control-flow constructs in the Intermediate Language. In practice, this is
equivalent to an explicit representation of a control-flow graph.
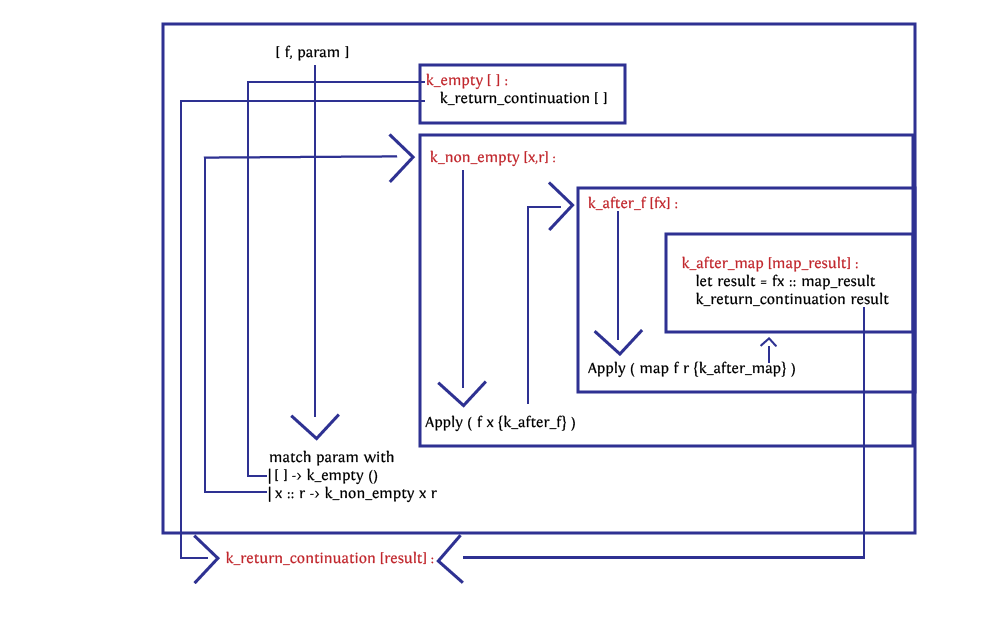
Here's an example using some hopefully intuitive syntax for the Flambda2
IR.
let rec map f = function
| [] -> []
| x :: r -> f x :: map f r
(* WARNING: FLAMBDA2 PSEUDO-SYNTAX INBOUND *)
let rec map
((f : <whatever_type1> ),
(param : <whatever_type2>))
{k_return_continuation : <return_type>}
{
let_cont k_empty () = k_return_continuation [] in
let_cont k_nonempty x r =
let_cont k_after_f fx =
let_cont k_after_map map_result =
let result = fx :: map_result in
k_return_continuation result
in
Apply (map f r {k_after_map})
in
Apply (f x {k_after_f})
in
match param with
| [] -> k_empty ()
| x :: r -> k_nonempty x r
}
Every let_cont binding declares a new sequence of instructions in the
control-flow graph, which can be terminated either by:
- calling a continuation (for example,
k_return_continuation) which takes a fixed number of parameters; - applying an OCaml function (
Apply), this function takes as a special parameter the continuation which it must jump to at the end of its execution. Unlike continuations, OCaml functions can take a number of arguments that does not match the number of parameters at their definition; - branching constructions like
match _ withandif _ then _ else _, in these cases each branch is a call to a (potentially different) continuation;
Notice that some boxes are nested to represent scoping relations: variables defined in the outer boxes are available in the inner ones.
To demonstrate the kinds of optimisations that such control-flow graphs allow us, see the following simple example:
Original Program:
let f cond =
let v =
if cond then
raise Failure
else 0
in
v, v
We then represent the same program using CPS in two steps, the first is the direct translation of the original program, the second is an equivalent program represented in a more compact form.
Minimal CPS transformation, using pseudo-syntax
(* showing only the body of f *)
(* STEP 1 - Before graph compaction *)
let_cont k_after_if v =
let result = v, v in
k_return_continuation result
in
let_cont k_then () = k_raise_exception Failure in
let_cont k_else () = k_after_if 0 in
if cond then k_then () else k_else ()
which becomes after inlining k_after_if:
(* STEP 2 - After graph compaction *)
let_cont k_then () = k_raise_exception Failure in
let_cont k_else () =
let v = 0 in
let result = v, v in
k_return_continuation result
in
if cond then k_then () else k_else ()
This allows us, by using the translation to CPS and back, to transform the original program into the following:
Optimized original program
let f cond =
if cond then
raise Failure
else 0, 0
As you can see, the original program is simpler now. The nature of the changes operated on the code are in fact not tied to a particular optimisation but rather the nature of the CPS transformation itself. Moreover, we do want to actively perform optimisations and to that extent, having an intermediate representation that is equivalent to a control-flow graph allows us to benefit from the huge amount of literature on the subject of static analysis of imperative programs which often are represented as control-flow graphs.
To be fair, in the previous example, we have cheated in how we have translated
the raise primitive. Indeed we used a simple continuation
(k_raise_exception) but we haven't defined it anywhere prior. This is
possible because our use of Double Barrelled CPS.
Double Barrelled CPS
In OCaml, all functions can not only return normally (Barrel 1) but also throw exceptions (Barrel 2), it corresponds to two different paths in the control-flow and we need the ability to represent it in our own control-flow graph.
Hence the name: Double Barrelled CPS, that we took from this
paper,
by Hayo Thielecke. In practice this only has consequences in four places:
- the function definitions must have two special parameters instead of one:
the exception continuation (
k_raise_exception) in addition to the normal return continuation (k_return_continuation); - the function applications must have two special arguments, reciprocally;
try ... withterms are translated using regular continuations with the exception handler (thewithpath of the construct) compiled to a continuation handler (let_cont);raiseterms are translated into continuation calls, to either the current function exception continuation (e.g. in case of uncaught exception) or the enclosingtry ... withhandler continuation.
The Flambda2 Term Language
This CPS form has directed the concrete implementation of the FL2 language.
We can see that the previous IRs have very descriptive representations, with
about 20 constructors for Clambda and 15 for Flambda while Flambda2 has
regrouped all these features into only 6 categories which are sorted by how
they affect the control-flow.
type expr =
| Let of let_expr
| Let_cont of let_cont_expr
| Apply of apply
| Apply_cont of apply_cont
| Switch of switch
| Invalid of { message : string }
The main benefits we reap from such a strong design choice are that:
- Code organisation is better: dealing with control-flow is only done when matching on full expressions and dealing with specific features of the language is done at a lower level;
- Reduce code duplication: features that behave in a similar way will have their common code shared by design;
Following up
The goal of this article was to show a fundamental design choice in Flambda2
which is using a CPS-based representation. This design is felt throughout the
Flambda2 architecture and will be mentioned and strengthened again in later
posts.
Flambda2 takes the Lambda IR as input, then performs CPS conversion,
followed by Closure conversion, each of them worth their own blog post, and
this produces the terms in the Flambda2 IR.
From there, we have our main optimisation pass that we call Simplify which
first performs static analysis on the term during a single Downwards Traversal,
and then rebuilds an optimised term during the Upwards Traversal.
Once we have an optimised term, we can convert it to the CMM IR and feed it
to the rest of the backend. This part is mostly CPS elimination but with added
original and interesting work we will detail in a specific snippet.
The single-pass design allows us to consider all the interactions between optimisations
Some examples of optimisations performed during Simplify:
- Inlining of function calls;
- Constant propagation;
- Dead code elimination
- Loopification, that is transforming tail-recursive functions into loops;
- Unboxing;
- Specialisation of polymorphic primitives;
Most of the following snippets will detail one of several parts of these optimisations.
Stay tuned, and thank you for reading !
Au sujet d'OCamlPro :
OCamlPro développe des applications à haute valeur ajoutée depuis plus de 10 ans, en utilisant les langages les plus avancés, tels que OCaml et Rust, visant aussi bien rapidité de développement que robustesse, et en ciblant les domaines les plus exigeants (méthodes formelles, cybersécurité, systèmes distribués/blockchain, conception de DSLs). Fort de plus de 20 ingénieurs R&D, avec une expertise unique sur les langages de programmation, aussi bien théorique (plus de 80% de nos ingénieurs ont une thèse en informatique) que pratique (participation active au développement de plusieurs compilateurs open-source, prototypage de la blockchain Tezos, etc.), diversifiée (OCaml, Rust, Cobol, Python, Scilab, C/C++, etc.) et appliquée à de multiples domaines. Nous dispensons également des [formations sur mesure certifiées Qualiopi sur OCaml, Rust, et les méthodes formelles] (https://training.ocamlpro.com/) Pour nous contacter : contact@ocamlpro.com.
Articles les plus récents
2024
2023
- Maturing Learn-OCaml to version 1.0: Gateway to the OCaml World
- The latest release of Alt-Ergo version 2.5.1 is out, with improved SMT-LIB and bitvector support!
- 2022 at OCamlPro
- Autofonce, GNU Autotests Revisited
- Sub-single-instruction Peano to machine integer conversion
- Statically guaranteeing security properties on Java bytecode: Paper presentation at VMCAI 23
- Release of ocplib-simplex, version 0.5
- The Growth of the OCaml Distribution
2022
2021